Science Fair Ideas

Circle calculator to calculate the area of a circle or the circumference of a circle given the radius.

You will need:

1. pencil to draw with
2. piece of 8-1/2" x 11" paper to draw on
3. a ruler or other straight edge to make lines
4. compass to draw circles.

This is how to find the center of a circle:

If you have something round, you can trace around it on the paper to make your circle. You can also make a circle of any size you want using the compass.

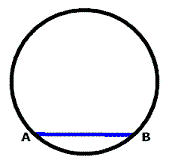
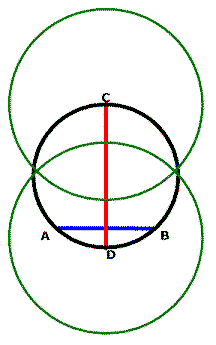
After you have a circle on your paper, draw a line segment with your straight edge inside the circle and label it AB. The exact location and size of the line AB is not important.

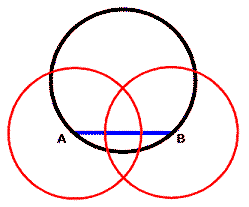
Use your compass to draw two equal circles with centers on the points A and B. The radii of the circles should be at least as long as 1/2 the length of AB so that the circles intersect each other similarly to those shown.

Note that the new circles can intersect inside or outside the original circle. It works either way but they must intersect.

Draw a line segment across the intersections of the two new circles and extend it so it touches the original circle. Label the new line inside the circle as CD.

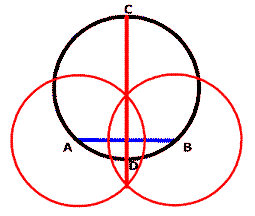
To make things a little easier to follow we removed the two red circles and part of the line. We don't need them anymore so you can erase yours if you wish.

The following is now true.....

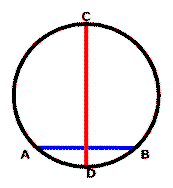
• The line CD is perpendicular to the line AB.
• The line CD bisects the line AB.
• The line CD is a diameter of the circle.

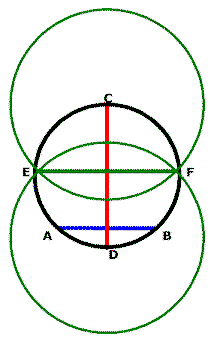
You will now repeat to line CD what you did to line AB.
You will bisect it and draw a line perpendicular to it.
The resulting line will be another diameter of the circle.

Use your compass to draw two equal circles with centers on the points C and D. The radii of the circles should be at least as long as 1/2 the length of CD so that the circles intersect each other similarly to those shown. Note that the new circles can intersect inside or outside the original circle. It works either way but they must intersect.

Draw a line segment across the intersections of the two new circles as far as the circle. Label the new line inside the circle as EF.

Again, to make things a little easier to follow you can erase the two green circles and part of the line EF if yours extends outside the circle. You can also remove the line AB. We don't need them anymore.

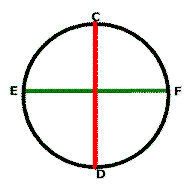
The following is true ....

• The line EF is perpendicular to the line CD.
• The line EF bisects the line CD.
• The line EF is the diameter of the circle.
• The point where EF intersects CD is the center of the circle!

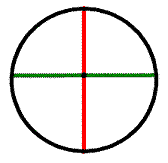
You now have a circle and you know exactly where the center is!!

Did you get it? Can you think of an easier way to find the center of a circle?

Further Research:

Circle calculator to calculate the area of a circle or the circumference of a circle given the radius.

This work is derived from Euclid's Elements starting at Book III Proposition 1.

Be sure to view the Introduction, and other pages, in this great work by D. E. Joyce.